Land-use (GLOBIOM)¶
Land-use dynamics are modelled with the GLOBIOM (GLobal BIOsphere Management) model, which is a partial-equilibrium model (Havlik et al., 2011 [25]; Havlik et al., 2014 [26]). GLOBIOM represents the competition between different land-use based activities. It includes a detailed representation of the agricultural, forestry and bio-energy sector, which allows for the inclusion of detailed grid-cell information on biophysical constraints and technological costs, as well as a rich set of environmental parameters, incl. comprehensive AFOLU (agriculture, forestry and other land use) GHG emission accounts and irrigation water use. For spatially explicit projections of the change in afforestation, deforestation, forest management, and their related CO2 emissions, GLOBIOM is coupled with the G4M (Global FORest Model) model (Kindermann et al., 2006 [45]; Kindermann et al., 2008 [43]; Gusti, 2010 [22]). The spatially explicit G4M model compares the income of forest (difference of wood price and harvesting costs, income by storing carbon in forests) with income by alternative land use on the same place, and decides on afforestation, deforestation or alternative management options. As outputs, G4M provides estimates of forest area change, carbon uptake and release by forests, and supply of biomass for bioenergy and timber.
As a partial equilibrium model representing land-use based activities, including agriculture, forestry and bioenergy sectors (see Fig. 19), production adjusts to meet the demand at the level of 30 economic regions (see list of the regions in Section Regions). International trade representation is based on the spatial equilibrium modelling approach, where individual regions trade with each other based purely on cost competitiveness because goods are assumed to be homogenous (Takayama and Judge, 1971 [104]; Schneider, McCarl et al., 2007 [97]). Market equilibrium is determined through mathematical optimization which allocates land and other resources to maximize the sum of consumer and producer surplus (McCarl and Spreen, 1980 [52]). As in other partial equilibrium models, prices are endogenous. The model is run recursively dynamic with a 10 year time step, going from 2000 to 2100. The model is solved using a linear programming solver and can be run on a personal computer with the GAMS software.
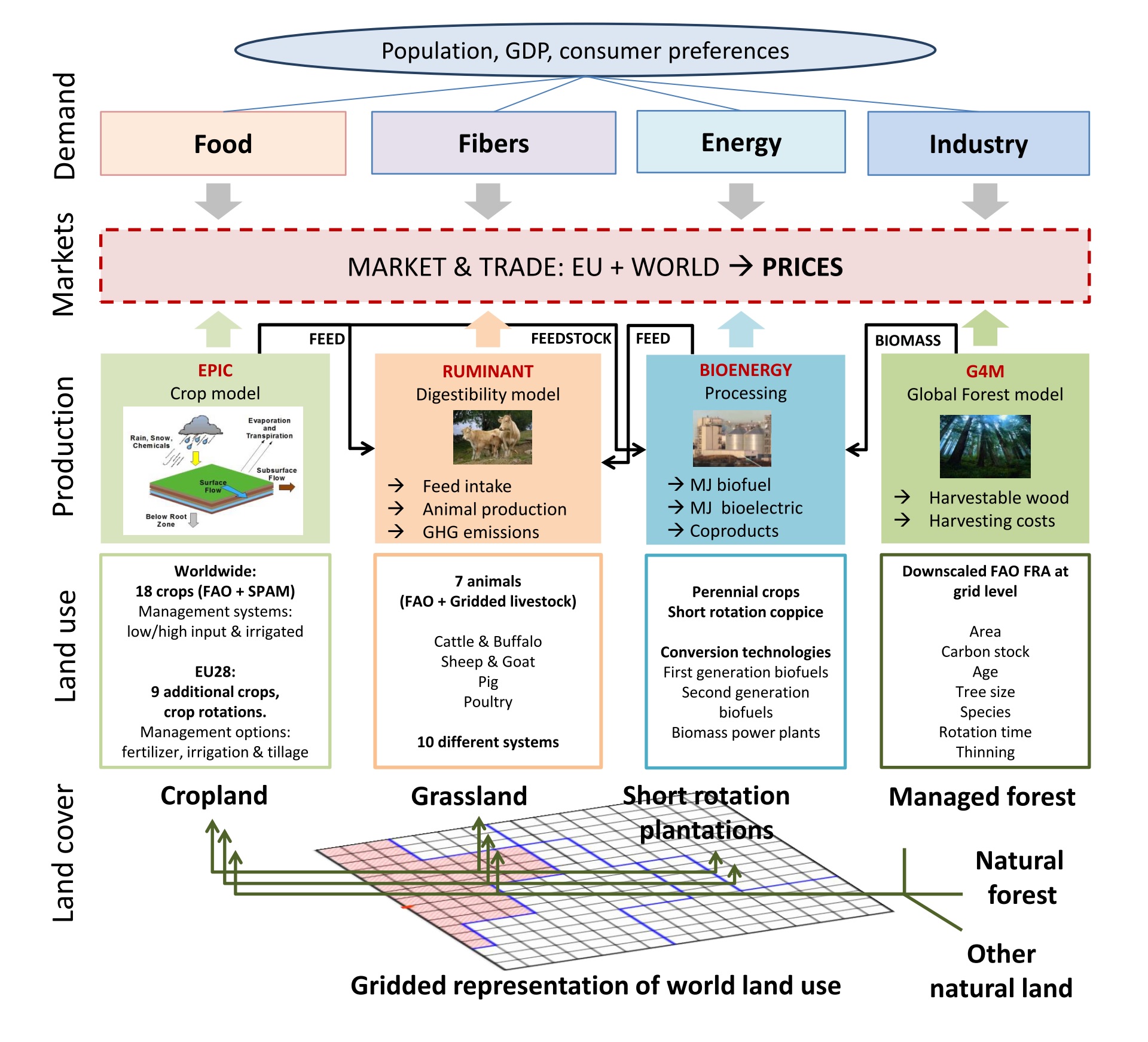
Fig. 19 GLOBIOM land use and product structure.¶